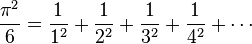
などは有名ですが、こういった式は分母がなかなか大きくならないために収束が遅く、世界最高記録を目指すようなケースでは論外です。
| トップ | よくある質問 | 作者ブログトップ | お問い合わせ・ご注文 |
円周率の高速な計算方法
よく新聞などで、「だれだれがスーパーコンピュータを使って円周率を世界最高記録のウン兆桁計算した」などという記事を見ます。
あれは、どういう計算式で求めているのでしょうか。
簡単な式では、
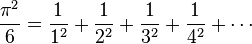
などは有名ですが、こういった式は分母がなかなか大きくならないために収束が遅く、世界最高記録を目指すようなケースでは論外です。
Wikipediaを見ると、現実に円周率を高速に求める場合には、収束の速いさまざまな式が用いられるようですが、ストーマの公式

などが有用なようです。
FullTr-11での円周率の計算では、マチンの公式
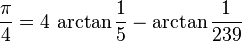
を用いています。
これをテイラー展開して第二項まで取ってやれば(正確にはarctan(1/239)の展開は第一項までで十分です)、3.1405...となり、3桁までは正しい結果が得られます。
実際にはFullTr-11は整数の加算と減算しかできませんので、展開後の式で両辺を整数倍して、分子の1を大きな整数にするなどの式変形を施し、かつ、命令や使用するメモリの量を減らす工夫をします。
動画ではROMの表示が止まって見える時間が長いですが、これは5で割る演算を行っている時間です。
この間に、中央下側のレジスタが乗っている基板の右上部分のLED表示を見ると、2進数で5が表示されていますが、これは割り算ルーチンにおける分母がここにあるためです。
動画の計算では3秒ちょっとかかっていますが、コードを工夫すれば実行時間は更に40%近く削減できるはずです。
あまり速すぎると動画的に面白くないですが。
PICやAVRで円周率を100桁まで求めたというような話も、ほとんどがマチンの公式を使うようです。
何桁まで計算できるかはRAMのサイズによりますが、FullTr-11では最大で2.75キロバイトまでRAMを拡張できるので、理屈の上では1400桁程度まで計算できるはずです。
マチンの公式の証明はいろいろあるようですが、最も簡単なものは、複素数を使う方法で、
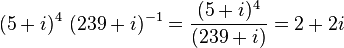
で両辺の各項をr exp(-i theta)の形式で書いて、複素平面内の角度を求めるという方法です。